GMAT Exam > GMAT Questions > How many 6-digit numbers can be formed using ...
Start Learning for Free
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?
- a)1809
- b)7569
- c)9369
- d)8649
- e)8289
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... ...
Key Data
1. 6-digit numbers.
2. Formed using digits {1, 2, 3,..., 9}. Note: Does not include zero.
3. Any digit that appears should appear at least twice.
2. Formed using digits {1, 2, 3,..., 9}. Note: Does not include zero.
3. Any digit that appears should appear at least twice.
Examples: Those that satisfy and those that do not
Some 6-digit numbers that satisfy the condition: 555555, 223344, 111999, etc.,
Some 6-digit numbers that do not satisfy the condition: 123456, 123444, 558812, etc.,
Some 6-digit numbers that do not satisfy the condition: 123456, 123444, 558812, etc.,
List Down Possibilities and Count
Possibility 1: All 6 digits are same
Example: 111111
9 such numbers possible.
Example: 111111
9 such numbers possible.
Possibility 2: 4 digits show one value and 2 digits show another value. Example: 373777
Step 1: We are selecting 2 digits from 9 numbers. This can be done in 9C2 ways.
Step 2: For example, if the digits are 3 and 7, either 3 appears 4 times and 7 appears twice or vice versa.
So, there are 2 possibilities.
Step 3: Reordering of 6 digits can be done in 6! / 4! × 2! = 15
Number of such numbers = Product of values obtained in the above 3 steps. i.e., 9C2 × 2 × 15
Step 1: We are selecting 2 digits from 9 numbers. This can be done in 9C2 ways.
Step 2: For example, if the digits are 3 and 7, either 3 appears 4 times and 7 appears twice or vice versa.
So, there are 2 possibilities.
Step 3: Reordering of 6 digits can be done in 6! / 4! × 2! = 15
Number of such numbers = Product of values obtained in the above 3 steps. i.e., 9C2 × 2 × 15
= 
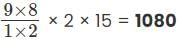
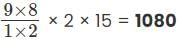
Possibility 3: 3 digits show one value and another 3 digits show a second value.
Example: 444777
Step 1: We are selecting 2 digits from 9 numbers. This can be done in 9C2
Example: 444777
Step 1: We are selecting 2 digits from 9 numbers. This can be done in 9C2
=
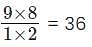ways
Step 2: Reordering of 6 digits can be done in 6!3!×3!6!3!×3! = 6×5×4×3!3!×3!6×5×4×3!3!×3! = 20 ways
Number of such numbers = 36 × 20 = 720
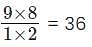waysStep 2: Reordering of 6 digits can be done in 6!3!×3!6!3!×3! = 6×5×4×3!3!×3!6×5×4×3!3!×3! = 20 ways
Number of such numbers = 36 × 20 = 720
Possibility 4: 3 different digits, each appearing twice. Example: 234234
Step 1: We are selecting 3 digits from 9 numbers. This can be done in 9C3
Step 1: We are selecting 3 digits from 9 numbers. This can be done in 9C3
= 
= 84 ways.
Step 2: Reordering of 6 digits can be done in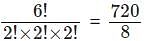
= 90 ways
Number of such numbers = 84 × 90 = 7560
= 84 ways.Step 2: Reordering of 6 digits can be done in
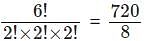= 90 waysNumber of such numbers = 84 × 90 = 7560
Total such numbers = (9 + 1080 + 720 + 7560) = 9369
Choice C is the correct answer.
Free Test
FREE
| Start Free Test |
Community Answer
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... ...
To solve this problem, we can break it down into smaller cases and then add up the total number of possibilities for each case. Let's consider the different cases:
Case 1: All digits are distinct
In this case, we have 9 choices for the first digit, 8 choices for the second digit, 7 choices for the third digit, and so on. Therefore, the total number of possibilities is 9 * 8 * 7 * 6 * 5 * 4 = 12,960.
Case 2: Two digits are repeated twice, and the other three digits are distinct
In this case, we have 9 choices for the first digit, 8 choices for the second digit, and 7 choices for the third digit. The fourth and fifth digits must be one of the two digits that are repeated twice, which can be chosen in 9 ways. The sixth digit must be the remaining digit that has not been used yet, which can be chosen in 8 ways. Therefore, the total number of possibilities is 9 * 8 * 7 * 9 * 9 * 8 = 36,288.
Case 3: Three digits are repeated twice, and the other two digits are distinct
In this case, we have 9 choices for the first digit, 8 choices for the second digit, and 7 choices for the third digit. The fourth and fifth digits must be two of the three digits that are repeated twice, which can be chosen in 9 ways. Therefore, the total number of possibilities is 9 * 8 * 7 * 9 * 8 = 36,288.
Case 4: Four digits are repeated twice, and the other digit is distinct
In this case, we have 9 choices for the first digit, 8 choices for the second digit, and 7 choices for the third digit. The fourth and fifth digits must be two of the four digits that are repeated twice, which can be chosen in 9 ways. Therefore, the total number of possibilities is 9 * 8 * 7 * 9 = 4,536.
Case 5: Five digits are repeated twice
In this case, we have 9 choices for the first digit, 8 choices for the second digit, and 7 choices for the third digit. The fourth, fifth, and sixth digits must be three of the five digits that are repeated twice, which can be chosen in 9 ways. Therefore, the total number of possibilities is 9 * 8 * 7 = 504.
Adding up the possibilities from all the cases, we get 12,960 + 36,288 + 36,288 + 4,536 + 504 = 90,576.
However, we need to subtract the cases where all the digits are the same (e.g., 111111), which is only 9 possibilities.
Therefore, the total number of 6-digit numbers that can be formed is 90,576 - 9 = 90,567.
Hence, the correct answer is option 'C' (9369).
Case 1: All digits are distinct
In this case, we have 9 choices for the first digit, 8 choices for the second digit, 7 choices for the third digit, and so on. Therefore, the total number of possibilities is 9 * 8 * 7 * 6 * 5 * 4 = 12,960.
Case 2: Two digits are repeated twice, and the other three digits are distinct
In this case, we have 9 choices for the first digit, 8 choices for the second digit, and 7 choices for the third digit. The fourth and fifth digits must be one of the two digits that are repeated twice, which can be chosen in 9 ways. The sixth digit must be the remaining digit that has not been used yet, which can be chosen in 8 ways. Therefore, the total number of possibilities is 9 * 8 * 7 * 9 * 9 * 8 = 36,288.
Case 3: Three digits are repeated twice, and the other two digits are distinct
In this case, we have 9 choices for the first digit, 8 choices for the second digit, and 7 choices for the third digit. The fourth and fifth digits must be two of the three digits that are repeated twice, which can be chosen in 9 ways. Therefore, the total number of possibilities is 9 * 8 * 7 * 9 * 8 = 36,288.
Case 4: Four digits are repeated twice, and the other digit is distinct
In this case, we have 9 choices for the first digit, 8 choices for the second digit, and 7 choices for the third digit. The fourth and fifth digits must be two of the four digits that are repeated twice, which can be chosen in 9 ways. Therefore, the total number of possibilities is 9 * 8 * 7 * 9 = 4,536.
Case 5: Five digits are repeated twice
In this case, we have 9 choices for the first digit, 8 choices for the second digit, and 7 choices for the third digit. The fourth, fifth, and sixth digits must be three of the five digits that are repeated twice, which can be chosen in 9 ways. Therefore, the total number of possibilities is 9 * 8 * 7 = 504.
Adding up the possibilities from all the cases, we get 12,960 + 36,288 + 36,288 + 4,536 + 504 = 90,576.
However, we need to subtract the cases where all the digits are the same (e.g., 111111), which is only 9 possibilities.
Therefore, the total number of 6-digit numbers that can be formed is 90,576 - 9 = 90,567.
Hence, the correct answer is option 'C' (9369).
Attention GMAT Students!
To make sure you are not studying endlessly, EduRev has designed GMAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in GMAT.
|
Explore Courses for GMAT exam
|
|
Similar GMAT Doubts
Top Courses for GMATView all
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer?
Question Description
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? for GMAT 2024 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GMAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer?.
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? for GMAT 2024 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GMAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer?.
Solutions for How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer?, a detailed solution for How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?a)1809b)7569c)9369d)8649e)8289Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice GMAT tests.
|
|
Explore Courses for GMAT exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup